Нейробиологи использовали классическую часть математики совершенно по-новому, чтобы изучить структуру нашего мозга.
Они обнаружили, что мозг наполнен многомерными геометрическими структурами, работающими в 11 измерениях.
Мы привыкли думать о мире в трехмерной перспективе, поэтому это может показаться немного сложным, но результаты этого исследования могут стать следующим важным шагом в понимании структуры человеческого мозга — самой сложной структуры.
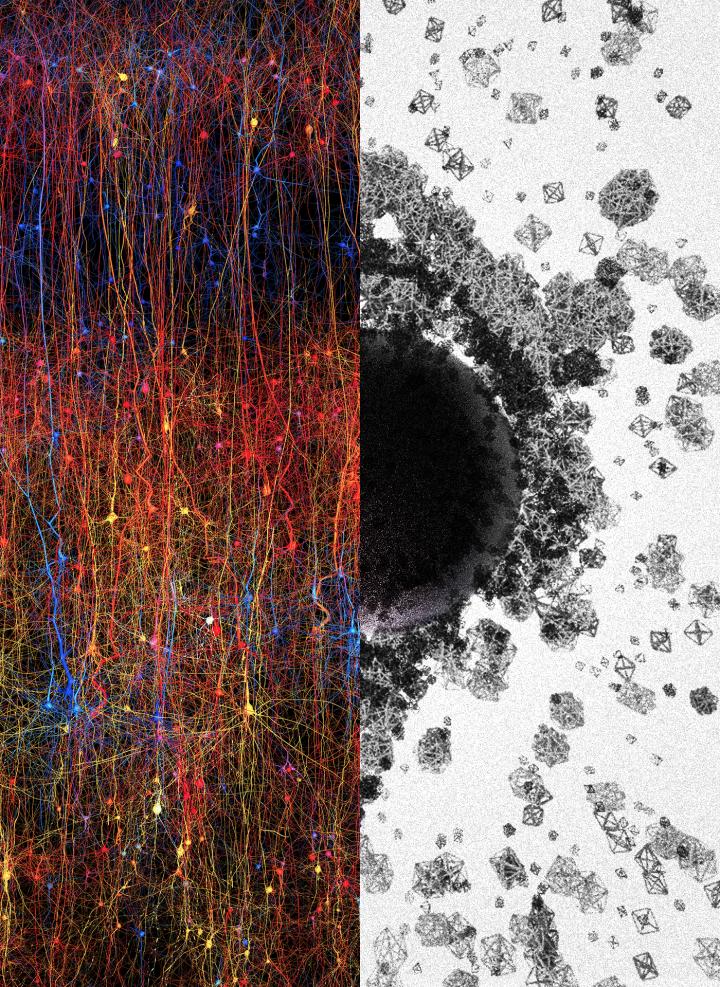
Слева — цифровая копия части неокортекса, наиболее развитой части мозга.
Справа — формы разных размеров и геометрии, в попытке представить структуры от 1 до 7 и более измерений.
«Черная дыра» в центре символизирует комплекс многомерных пространств или полостей.
Исследователи из проекта Blue Brain Project сообщают, что группы нейронов, связанных с такими полостями, обеспечивают недостающее звено между нейронной структурой и функцией в их новом исследовании, опубликованном в Frontiers in Computational Neuroscience.
Кредит изображения: Проект Blue Brain.
Эта модель мозга была создана группой исследователей из проекта Blue Brain Project, швейцарской исследовательской инициативы, посвященной созданию реконструкции человеческого мозга на базе суперкомпьютера.
Команда использовала алгебраическую топологию, раздел математики, используемый для описания свойств объектов и пространств независимо от того, как они меняют форму.
Они обнаружили, что группы нейронов соединяются в «клики», и что количество нейронов в клике приводит к ее размеру как геометрическому объекту большой размерности (понятие математического измерения, а не пространственно-временного).
«Мы нашли мир, о котором никогда не мечтали», — сказал ведущий исследователь, нейробиолог Генри Маркрам из института EPFL в Швейцарии.
«Есть десятки миллионов этих объектов даже в небольшой частичке мозга, охватывающей семь измерений. В некоторых сетях мы даже обнаружили структуры с 11 измерениями».
Для ясности — это не то, как вы думаете о пространственных измерениях (наша Вселенная имеет три пространственных измерения плюс одно временное измерение), вместо этого это относится к тому, как исследователи смотрели на клики нейронов, чтобы определить, насколько они связаны.
«Сети часто анализируются с точки зрения групп узлов, которые связаны между собой все со всеми, известных как клики. Количество нейронов в клике определяет ее размер или, более формально, ее размер», — поясняют исследователи в статье.
По оценкам, человеческий мозг состоит из 86 миллиардов нейронов , каждая клетка которых соединяется сетью во всех возможных направлениях, образуя обширную сотовую сеть, которая каким-то образом делает нас способными мыслить и осознанно.
С таким огромным количеством подключений, с которыми нужно работать, неудивительно, что мы до сих пор не до конца понимаем, как работает нейронная сеть мозга.
Но математическая основа, созданная командой, приближает нас на шаг ближе к дню создания цифровой модели мозга.
Для выполнения математических тестов команда использовала подробную модель неокортекса, опубликованную командой Blue Brain Project еще в 2015 году .
Неокортекс считается самой недавно развившейся частью нашего мозга и той, которая участвует в некоторых из наших функций высшего порядка, таких как познание и сенсорное восприятие.
Разработав математическую схему и проверив ее на некоторых виртуальных стимулах, команда также подтвердила свои результаты на реальной мозговой ткани крыс.
По словам исследователей, алгебраическая топология предоставляет математические инструменты для различения деталей нейронной сети как в крупном плане на уровне отдельных нейронов, так и в более широком масштабе структуры мозга в целом.
Соединяя эти два уровня, исследователи могли различать многомерные геометрические структуры в мозге, образованные наборами тесно связанных нейронов (клик) и пустых пространств (полостей) между ними.
«Мы обнаружили удивительно большое количество и разнообразие многомерных направленных «клик структур» и полостей, которые ранее не наблюдались в нейронных сетях, ни биологических, ни искусственных», — написала команда в исследовании .
«Алгебраическая топология подобна телескопу и микроскопу одновременно», — сказала одна из команды, математик Кэтрин Хесс из EPFL .
«Он может увеличивать масштаб сети, чтобы находить скрытые структуры, деревья в лесу и одновременно видеть пустые пространства и поляны».
Эти полости или полости кажутся критически важными для работы мозга. Когда исследователи дали стимул своей виртуальной мозговой ткани, они увидели, что нейроны реагируют на него высокоорганизованным образом.
«Это как если бы мозг реагировал на стимул, строя [и] затем разрушая башню из многомерных блоков, начиная с стержней (1D), затем досок (2D), затем кубиков (3D), а затем более сложных геометрических фигур. с 4D, 5D и т.д. «, — сказал один из членов группы, математик Ран Леви из Абердинского университета в Шотландии.
«Развитие активности через мозг напоминает многомерный замок из песка, который материализуется из песка, а затем распадается».
Эти результаты дают новую захватывающую картину того, как мозг обрабатывает информацию, но исследователи отмечают, что пока не ясно, что заставляет клики и полости формироваться в таких весьма специфических образах.
Потребуется дополнительная работа, чтобы определить, как сложность этих многомерных геометрических фигур, формируемых нашими нейронами, соотносится со сложностью различных когнитивных задач.
Но это определенно не последнее, что мы услышим о том, что алгебраическая топология может дать нам об этом самом загадочном из человеческих органов — мозге.
Исследование было опубликовано в Frontiers of Computational Neuroscience.












